Решение задач с помощью таблиц
1. Володя, Костя, Дима, Саша играли в хоккей. Один из них не забил ни одного гола, другой – один гол, третий – два гола, четвертый – четыре гола. Известно, что Костя забил меньше четырех голов. Володя, как ни старался, все время не попадал в ворота, а Дима забил один гол. Кто сколько забил голов?
2. Маргарита. Они очень любили посмеяться. Придворные знали, сколько смеялась каждая принцесса каждый день. Принцессы смеялись 2, 5, 7, 10 минут. Наталия не могла смеяться дольше 2 минут, Маргарита смеялась 10 минут, Ольга смеялась меньше Дианы. Сколько минут смеялась каждая принцесса?
3. Встретились три подруги Белова, Краснова и Чернова. На одной было чёрное платье, на другой красное, а на третьей белое платье. Девочка в белом платье сказала Черновой: «Нам троим надо поменяться платьями, а то цвета наших платьев не соответствуют нашим фамилиям». Кто в какое платье был одет?
4. Катя, Соня, Галя и Тамара родились 2 марта, 17 мая, 2 июля и 20 марта. Соня и Галя родились в одном месяце, а у Гали и Кати дни рождения обозначаются одинаковыми числами. Кто когда родился?
5. Кондратьев, Иванов и Жуков живут на одной улице. Один из них – столяр, другой – маляр, третий – водопроводчик. Недавно Иванов хотел попросить столяра, который был его старым знакомым, сделать кое-что для своей квартиры, но ему сказали, что столяр работает в доме водопроводчика. Известно также, что Жуков никогда не слышал об Иванове. У кого какая профессия?
6. Боря, Витя, Гриша и Егор встретились и подружились в летнем лагере «Артек». Они приехали сюда из разных городов: один – из Твери, другой – из Омска, третий – из Екатеринбурга, четвертый – из Казани. Из какого города приехал каждый, если известно, что:
1) Боря и мальчик из Казани жили в одной комнате;
2) Боря никогда не был ни в Твери, ни в Екатеринбурге;
3) Гриша играл в волейбол в одной команде с мальчиком из Твери, а против них обычно сражался их приятель из Казани;
4) Егор и мальчик из Твери увлекались игрой в шахматы.
7. Пять друзей – Дима, Саша, Коля, Сережа и Юра – решили купить себе удочки. Удочки были пяти цветов: красного, синего, белого, зеленого и черного. Известно, что:
1) Дима любит красный и синий цвета;
2) Сереже нравились синяя и зеленая удочки;
3) Коля купил зеленую удочку;
4) Юра отдавал предпочтение красной, синей и черной удочкам.
Кто какую удочку купил, если у всех были удочки разного цвета?
8. Живут-поживают пять зайчат: Прыгунчик, Ушастик, Тишка, Зайка и Беляк, и у каждого есть мячик. Цвета мячиков такие: синий, зеленый, красный, желтый и оранжевый. У Ушастика мячик желтого цвета, а у Зайки – не зеленый, не синий и не красный. У Прыгунчика был бы синий мячик, если бы у Беляка был зеленый мячик, но у Беляка мячик другого цвета. Беляк не любит игрушки синего цвета. У кого какой мячик?
9. Гонщики приехали на авторалли на своих машинах. У Джека машина красная, у Питера – не черная, не синяя и не голубая, у Майка есть черная и синяя машины, у Алексея есть машины всех перечисленных цветов, а у Берри есть машины белого и синего цветов. У кого какого цвета была машина, если все юноши были на машинах разного цвета?
10. Света, Марина, Андрей, Кирилл и Юра держат домашних животных. У каждого либо кошка, либо собака, либо попугай. Девочки не держат собак, а мальчики попугаев. У Светы нет кошки. У Светы и Марины разные животные. У Марины и Андрея – одинаковые. У Андрея и Кирилла – разные. У Кирилла и Юры – одинаковые. Какие животные у каждого.
11. В школе учатся 4 талантливых мальчика: Иванов, Петров, Сидоров и Андреев. Один из них – будущий музыкант, другой преуспел в бальных танцах, третий – солист хора мальчиков, четвертый подает надежды как художник. О них известно, что Иванов и Сидоров присутствовали в зале консерватории, когда там солировал в хоре мальчиков певец. Петров и музыкант вместе позировали художнику. Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться с Ивановым. Иванов не знаком с Сидоровым, т.к. они учатся в разных классах и в разные смены. Кто чем увлекается?
12. Маша, Оля, Лена и Валя – замечательные девочки. Каждая из них играет на каком-нибудь музыкальном инструменте и говорит на одном из иностранных языков. Инструменты и языки у них разные. Маша играет на рояле. Девочка, которая говорит по-французски, играет на скрипке. Оля играет на виолончели. Маша не знает итальянского языка, а Оля не владеет английским. Лена не играет на арфе, а виолончелистка не говорит по-итальянски. Нужно определить, на каком инструменте играет каждая из девочек и каким иностранным языком она владеет.
13. Жили три молодых человека – Андрей, Бронислав и Борис. Один из них – аптекарь, другой – бухгалтер, третий – агроном. Один живет в Бобруйске, другой – в Архангельске, третий – в Белгороде. Требуется выяснить, кто, где живет и у кого какая профессия. Известно лишь, что Борис бывает в Бобруйске наездами и то весьма редко, хотя все его родственники живут в этом городе. У двоих из этих людей названия профессий и городов, в которых они живут, начинаются с той же буквы, что и имена. Жена аптекаря приходится Борису младшей сестрой.
Дополнительный материал можно найти здесь:
1. http://mtcol.ru/elt/logics/project/p18aa1.html
2.http://mmmf.msu.ru/archive/20052006/z5/11.html
Задачи со спичками
1. Положите 3 спички на стол так, чтобы их головки не касались поверхности стола и друг друга.
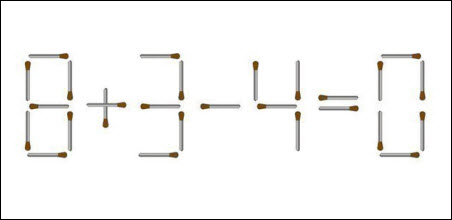2. Нужно переложить одну спичку так, чтобы получилось верное равенство.
3. Двенадцать спичек выложены так, как показано на рисунке. Сколько здесь квадратов? Выполните следующие задания: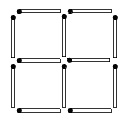
а) уберите 2 спички так, чтобы образовалось 2 неравных квадрата;
б) переложите 3 спички так, чтобы образовалось 3 равных квадрата;
в) переложите 4 спички так, чтобы образовалось 10 квадратов.
4. Сделайте из 5 спичек 5 одинаковых треугольников и 1 пятиугольник.
5 Из 10 спичек составьте три квадрата двумя способами.
6. В трёх кучках лежат спички, по 10 спичек в каждой. Играют Аня и Вова. Ход состоит в том, что игрок забирает несколько спичек, но только из какой-либо одной кучки. Начинает Аня. Побеждает тот, кому достанется последняя спичка. Может ли кто-нибудь из игроков играть так, чтобы наверняка выиграть, как бы ни старался другой?
7. Расположите 6 спичек так, чтобы получилось 4 треугольника.
8. И "бокал" (см. левый рисунок), и "рюмка" (см. правый рисунок)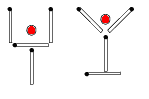 
составлены из четырех спичек. Внутри каждого "сосуда" — вишенка. Как нужно переместить "бокал" и "рюмку", переложив по две спички в каждом из них, чтобы вишенки оказались снаружи?
9. 48 спичек разложены на три неравные кучки. Если из первой кучки переложить во вторую столько спичек, сколько в этой второй кучке имелось, затем из второй в третью переложить столько, сколько в этой третьей перед тем будет находиться, и из третьей переложить в первую столько спичек, сколько в этой первой кучке будет тогда иметься, то спичек во всех кучках станет одинаковое количество. Сколько спичек было в каждой кучке первоначально?
10. Переложите одну спичку так, что бы верное равенство так и осталось верным. 
11. Из спичек составлено неверное равенство (см. рисунок). Переставьте одну спичку так, чтобы равенство стало верным.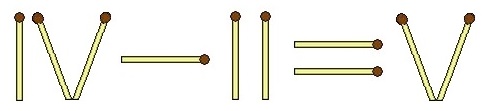
12. Двадцать четыре спички выложены так, как показано на рисунке. Сколько здесь квадратов? Выполните следующие задания:
а) уберите 4 спички так, чтобы образовалось 5 равных квадратов;
б) уберите 6 спичек так, чтобы образовалось 5 равных квадратов;
в) переложите 12 спичек так, чтобы образовалось 2 равных квадрата;
г) убери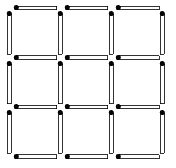
те 8 спичек так, чтобы образовалось 4 равных квадрата;
д) уберите 8 спичек так, чтобы образовалось 3 квадрата;
е) уберите 8 спичек так, чтобы образовалось 2 квадрата.
13. Переложите 4 спички, чтобы получилось 15 квадратов.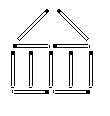
Дополнительный материал можно найти здесь:
1. https://ollforkids.ru/spichki/
2. http://www.treningmozga.com/tasks/matches_01.html
«Хвосты и ноги»
1. На детской площадке 8 двух- и трёх - колёсных велосипедов. Всего у них 21 колесо. Сколько было 2-х и 3-х колесных велосипедов на площадке?
2. В клетке кролики и фазаны, всего 35 голов и 94 ноги. Сколько в клетке кроликов и сколько фазанов?
3. Мальчик собрал в коробку жуков и пауков – всего 8 штук и 54 ноги. Сколько жуков и сколько пауков?
4. Грузовые автомобили имеют по 6 колёс, а легковые по 4 колеса. Сколько, каких автомобилей в гараже, если колёс всего 3024?.
5. Через мост за день прошло 40 автомобилей и велосипедов. Всего проехало 100 колес. Просчитай, сколько проехало отдельно автомобилей и велосипедов, если у велосипеда 2 колеса, а у автомобиля 4 колеса?
6. Магазин получил со склада 1000 линеек по 20 см и 30 см. общая длина линеек 220 м. Сколько 20-сантиметровых линеек получил магазин?
7. В учреждении 14 столов с одним, двумя и тремя ящика. Всего 25 ящиков. Столов с одним ящиком столько, сколько с двумя и тремя вместе. Сколько столов с тремя ящиками?
8.
По тропинке вдоль кустов
Шло 11 хвостов.
Сосчитать я также смог,
Что шагало 30 ног.
Это вместе шли куда-то
Петухи и поросята.
А теперь вопрос таков:
«Сколько было петухов?»
И узнать я был бы рад,
Сколько было поросят?
9. На корабле «Пиратское счастье» несколько кошек, матросов, кок и одноногий капитан. У всех вместе взятых 15 голов и 41 нога. Сколько на корабле было кошек?
10. На поляне ребята пасут жеребят. Если пересчитать ноги ребят и жеребят, то их будет 74, а если считать головы, то – 22. сколько на лугу жеребят?
11. Десяти собакам и кошам дали 56 галет. Каждой собаке досталось 6 галет, каждой кошке 5. сколько было собак и кошек?
12. Для туристов купили 100 билетов на сумму 340 рублей. Билеты стали 3 руб. и 4 руб. сколько закуплено билетов по 3 руб. и сколько по 4 руб.?
13. В клетке находятся цыплята и кролики. У них 15 голов и 36 ног. Сколько в клетке цыплят и сколько кроликов?
14. На веточке сирени 35 цветков, у которых по 4 или 5 лепестков. Всего лепестков 15. Сколько цветков с 5 лепестками?
15. У котенка на лапе 5 когтей, у цыплёнка 4. во дворе находится 10 котят и цыплят, а когтей у всей у них 104. Сколько котят во дворе?
16. В театре билеты продаются по 30 руб. и 40 руб. всего в театре 12 рядов по 25 мест в каждом. Общая стоимость всех билетов 10000 руб. сколько билетов продаётся по 40 руб.?
17. На каждой из 10 карточек Коля нарисовал треугольник или квадрат. Всего он провел 36 отрезков. Сколько квадратов он начертил?
18. По пустыне идет караван верблюдов, всего 40. У них 57 горбов. Сколько в караване одно – и двугорбых верблюдов?
19. Один человек видит и считает ноги верблюдов, другой – горбы. Первый насчитал 440 ног, второй – 160 горбов. Сколько в караване двугорбых верблюдов?
20. В гараже стояли машины и мотоциклы с коляской, их вместе 18. У них 65 колес. Сколько мотоциклов с коляской стояло в гараже, если у мотоцикла 3 колеса, а у машины 4?
21. В поход пошли 20 человек: мужчины, женщины и дети. Каждый мужчина нес груз 20 кг, каждая женщина – 5 кг, а каждый из детей – 3 кг. Все вместе несли груз массой 137 кг. Сколько мужчин, сколько женщин и сколько детей пошли в поход?
23. У бабушки Лизы – внуки и поросята. Сколько ребят и сколько поросят, если на всех приходится 6 хвостов и 30 ног?
Задачи на переливание
1. Для разведения картофельного пюре быстрого приготовления "Зеленый великан" требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?
2. Как с помощью 2-литровой и 5-литровой банок отмерить ровно 1 литр?
3. Как, имея пятилитровое ведро и девятилитровую банку, набрать из реки ровно три литра воды?
4. Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?
5. Есть два кувшина емкостью 5 л и 9 л. Нужно набрать из источника 7 л воды, если можно пользоваться только кувшинами.
6. У Марьи есть 2 кувшина объёмом 8 и 3 литра. В восьмилитровом кувшине налит весь имеющийся у Марьи кисель. Как отмерить 2 литра киселя? Все излишки киселя можно отдать Коту Баюну, который просто обожает это лакомство.
7. В кастрюле налито 8 литров супа. Есть также пустые 3-х и 5-тилитровая банки. Требуется отмерить 4 литра супа. Как это сделать, если суп нельзя проливать?
8. Как, имея два ведра 14 и 15 литров, набрать из реки 7 литров воды?
Убедитесь, что с помощью этих ведер можно набрать любое количество литров, выраженное натуральным числом меньше 14.
9. Имеются два сосуда вместимостью 17 литров и 5 литров. Как с помощью этих сосудов налить из водопроводного крана 13 литров воды?
10. В распоряжении имеется 2 емкости объемом 7л и 11л, а также кран с водой. Какое наименьшее число переливаний необходимо для того, чтобы отмерить 2 литра?
11. Есть 5 кастрюль. Из них - 4 по 4 литра и 1 по 2 литра. В первой кастрюле 1 литр воды, во второй 2 литра, в третьей 3 литра, в четвёртой 4 литра, а пятая кастрюля (которая вмещает 2 литра) пустая. Как нужно перелить кипящую воду для варки пельменей так, чтобы во всех кастрюлях было по 2 литра и за 4 переливания?
12. Можно ли разлить 50 литров бензина по трём бакам так, чтобы в первом баке было на 10 литров больше, чем во втором, а после переливания 26 литров из первого бака в третий в третьем баке стало столько же бензина, сколько во втором?
13. Есть три бидона емкостью 14 л, 9 л и 5 л. В большем бидоне 14 литров молока, остальные бидоны пусты. Как с помощью этих сосудов разлить молоко пополам?
14. Как, имея лишь 2 сосуда емкостями 5 л и 7 л, налить из водопроводного крана 6 л воды?
15. Как с помощью 7-литрового ведра и 3-литровой банки налить в кастрюлю ровно 5 л воды?
16. Как, имея 2 ведра емкостями 4 л и 9 л, налить из водопроводного крана 6 л воды?
17. Имеется 2 типа песочных часов: одни отмеряют 7 мин, а другие – 11 мин. Как с их помощью отмерить 15 мин, необходимых для того, чтобы сварить вкрутую яйцо?
18. В бочке 28 л бензина. Имеется 2 ведра емкостью по 7 л, в которые нужно налить по 6 л бензина. Кроме того, есть черпак емкостью 4 л. Как можно осуществить разлив?
19. В первый сосуд вмещается 9 л воды, во второй — 5 л, а в третий — 3 л. Первый сосуд наполнен водой, а остальные — пусты. Как с их помощью отлить 7 л воды?
20. Каким образом можно принести из реки ровно 6 л воды, если имеется только 2 ведра: одно — емкостью 4 л, другое — 9 л?
21. Бидон емкостью 10 л наполнен молоком. Требуется перелить из этого бидона 5 л в 7-литровый бидон, используя при этом еще один, 3-литровый. Как это сделать?
22. В бочке 18 л бензина. Имеется два ведра по 7 л, в которые нужно налить по 6 л бензина, и черпак, объем которого равен 4 л. Как можно осуществить разлив?
23. Как разделить поровну между двумя соседями 12 л хлебного кваса, который находится в 12-литровом сосуде, используя 8- и 3-литровый сосуды?
24. Как с помощью двух сосудов емкостями 7 л и 4 л разделить поровну молоко, находящееся в 12-литровом бидоне?
25. Можно ли с помощью двух сосудов емкостями 9 л и 11 л набрать из крана 10 л воды?
26. В один стакан налито 5 ложек чая, а в другой — 5 ложек молока. Ложку молока перелили из второго стакана в первый, затем тщательно все перемешали и л о леку чая с молоком перелили обратно во второй стакан. Чего оказалось больше: чая во втором стакане или молока — в первом?
27. Даны 3 емкости, объемы которых равны соответственно 20, 11 и 9 л. Наибольший сосуд наполнен водой. Как разделить эту жидкость на две равные части, используя два других сосуда?
28. Даны 3 емкости, объемы которых равны соответственно 16, 9 и 7 л. Наибольший сосуд наполнен водой. Как разделить эту жидкость на две равные части, используя два других сосуда?
29. Даны 3 емкости, объемы которых равны соответственно 18, 11 и 7 л. Наибольший сосуд наполнен водой. Как разделить эту жидкость на две равные части, используя два других сосуда?
30. Можно ли решить задачу, подобную предыдущим, для случая 10, 6 и 4 л?
31. В бочке не менее 10 л бензина. Как отлить из нее 6 л с помощью 9-литрового ведра и 5-литрового бидона?
32. В бочке не менее 13 ведер бензина. Как отлить из нее 8 ведер с помощью 9-ведерной и 5-ведерной бочек?
33. Имеется 3 бочонка вместимостью 6, 3 и 7 л. В первом и третьем содержится соответственно 4 и 6 л кваса. Требуется, пользуясь только этими тремя бочонками, разделить квас поровну на две части. Как это сделать?
34. В трех кучках находится 22,14 и 12 орехов. Требуется путем трех перекладываний уравнять число орехов в каждой кучке, соблюдая при этом условие: из каждой кучки разрешается перекладывать в другую лишь столько орехов, сколько их в этой второй кучке.
35. В трех кучках находится 11,7 и 6 орехов. Требуется за три хода уравнять число орехов во всех кучках, соблюдая при этом условие: из каждой кучки разрешается перекладывать в другую лишь столько орехов, сколько их в этой второй кучке.
36. В походе приготовили ведро компота. Как, имея банки, вмещающие 500г и 900г воды, отливать компот порциями по 300 г?
37. Нефтяники пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6 литров нефти. В распоряжении имеется 9-литровый и 4-литровый сосуды. Как с помощью этих сосудов набрать 6 литров?
38. Поставили самовар, а потом 7 раз садились пить чай и каждый раз выпивали половину имеющейся в нем воды и еще полстакана, после чего воды не осталось. Сколько воды было в самоваре перед чаепитием?
39. Имеются две одинаковые чашки, одна с чаем, а другая – пустая. Из первой переливают половину имеющегося в ней чая во вторую, затем из второй переливают треть имеющегося в ней чая в первую, затем из первой переливают четверть имеющегося в ней чая во вторую и т.д. Сколько чая окажется в каждой из чашек после 100 переливаний?
40. Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
41. Две группы альпинистов готовятся к восхождению. Для приготовления еды они используют примусы, которые заправляют бензином. В альплагере имеется 10-литровая канистра бензина. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить бензин в два сосуда по 5 литров в каждом?
Признаки делимости
1. Вовочка написал в тетради число 65349*0712 в качестве примера числа, которое делится: а) на 9; б) на 3. (На месте звёздочки когда-то была написана цифра, а теперь там пятно от сладкого чая.) Помогите Вовочке восстановить пропущенную цифру. Укажите все возможные варианты!
2. Запишем подряд цифры от 1 до 9, получим число 123456789. Простое оно или составное? Изменится ли ответ в задаче, если каким-то образом поменять порядок цифр в этом числе?
3. Делится ли число 32561698 на 12? Решите эту задачу:
а) с помощью признака делимости на 4;
б) с помощью признака делимости на 3.
4. Даша и Таня по очереди выписывают на доску цифры шестизначного числа. Сначала Даша выписывает первую цифру, затем Таня — вторую, и так далее. Таня хочет, чтобы полученное в результате число делилось на три, а Даша хочет ей помешать. Кто из них может добиться желаемого результата независимо от ходов соперника?
5. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, составленное из цифр — названий этих городов, делится на 3. Можно ли добраться из города 1 в город 9?
6. Чтобы открыть сейф, нужно ввести код — семизначное число, состоящее из двоек и троек. Сейф откроется, если двоек в коде больше, чем троек, а сам код делится и на 3, и на 4. Какой код может открывать сейф?
7. Замените звездочки в записи числа 72*4* цифрами так, чтобы это число делилось на 45. Укажите все возможные варианты!
8. а)Докажите, что произведение двух последовательных чётных чисел всегда делится на 8.
б) Может ли произведение четырех последовательных натуральных чисел оканчиваться на 116?
9. Докажите, что из любых семи различных цифр можно составить число, которое делится на четыре.
10. Может ли произведение числа и суммы его цифр равняться 4704?
11. Может ли натуральное число, записываемое с помощью 10 нулей, 10 единиц и 10 двоек, быть квадратом некоторого другого натурального числа?
12. Натуральное число В обладает следующим свойством: для любого числа A, которое делится на В, на В также делятся и все числа, полученные из А перестановкой цифр. Докажите, что В может быть равно только 1, 3 или 9.
13. Ковбой Билл зашёл в бар и попросил у бармена бутылку виски за 3 доллара и шесть коробков непромокаемых спичек, цену которых он не знал. Бармен потребовал с него 11 долларов 80 центов (1 доллар = 100 центов), и в ответ на это Билл вытащил револьвер. Тогда бармен пересчитал стоимость покупки и исправил ошибку. Как Билл догадался, что бармен пытался его обсчитать?
14. Петя собирается все 90 дней каникул провести в деревне и при этом каждый второй день (то есть через день) ходить купаться на озеро, каждый третий — ездить в магазин за продуктами, а каждый пятый день — решать задачи по математике. (В первый день Петя сделал и первое, и второе, и третье и очень устал.) Сколько будет у Пети «приятных» дней, когда нужно будет купаться, но не нужно ни ездить в магазин, ни решать задачи? Сколько «скучных», когда совсем не будет никаких дел?
15. Найдите наибольшее четырёхзначное число, все цифры которого различны и которое делится на 2, 5, 9 и 11.
16. В клетках шахматной доски записаны в произвольном порядке натуральные числа от 1 до 64 (в каждой клетке записано ровно одно число и каждое число записано ровно один раз). Может ли в ходе шахматной партии сложиться ситуация, когда сумма чисел, записанных в клетках, занятых фигурами, ровно вдвое меньше суммы чисел, записанных в клетках, свободных от фигур?
17. Двое по очереди расставляют цифры (возможно, повторяющиеся) в таблицу 1x9. Если получившееся девятизначное число делится на а) 9 б) 11, то выигрывает первый игрок, иначе выигрывает второй. Кто выиграет при правильной игре.
Дополнительный материал можно найти здесь:
https://ankolpakov.ru/2018/09/02/olimpiadnye-zadachi-na-delimost/
Задачи на инварианты
Инвариант в математике – это свойство некоторого класса (множества) математических объектов оставаться неизменными при преобразованиях определенного типа. В качестве инварианта может использоваться четность или раскраска. В задачах о сумме цифр чаще всего используются остатки от деления на 3 или 9.
Полуинвариант - величина, изменяющаяся только в одну сторону (т. е. которая может только увеличиваться или только уменьшаться). Понятие полуинварианта часто используется при доказательстве остановки процесса.
Нередко встречаются задачи, в которых спрашивается, можно ли в результате некоторых действий получить тот или иной результат. Основным методом решения подобных задач является нахождение свойства исходного объекта, которое не меняется после выполнения таких действий, — это и есть инвариант. Если конечный объект задачи не обладает найденным свойством, то он, очевидно, не может быть получен в результате этих действий из исходного объекта.
1. Саша написал на листе бумаги число 10. Пятнадцать одноклассников передают лист друг другу, и каждый либо прибавляет к числу, либо отнимает от него единицу. Может ли в результате получиться число 0?
2. В одной клетке квадратной таблицы 4x4 стоит знак минус, а в остальных стоят плюсы. Разрешается одновременно менять знак во всех клетках, расположенных в одной строке или в одном столбце. Докажите, что, сколько бы мы ни проводили таких перемен знака, нам не удастся получить таблицу из одних плюсов.
3. На доске записаны 15 чисел: 8 нулей и 7 единиц. Необходимо 14 раз подряд выполнить следующую операцию: зачеркнуть любые два числа, и, если они одинаковые, то дописать к оставшимся числам нуль, а если разные — то единицу. Какое число останется на доске?
4. Можно ли разменять купюру достоинством 50 рублей с помощью 15 монет достоинством 1 и 5 рублей?
5. 2015 человек выстроились в шеренгу. Всегда ли можно их расставить по росту, если за один ход разрешается переставлять только 2 людей, стоящих через одного?
6. 16 корзин расположили по кругу. Можно ли в них разложить 55 дынь так, чтобы количество дынь в любых двух соседних корзинах отличалось на 1?
Принцип Дирихле
В несерьёзной форме принцип Дирихле гласит: «Нельзя посадить 7 кроликов в 3 клетки, чтобы в каждой было не больше 2 кроликов».
В математической терминологии принцип Дирихле звучит так: если n+1 элемент разбит на n множеств, то, по крайней мере, одно множество содержит не менее двух элементов.
Принципом Дирихле традиционно называют следующее утверждение: если в 50 клетках сидит 51 кролик, то, по крайней мере, в одной клетке сидит не менее двух кроликов.
Доказательство этого принципа очевидно. Действительно, пусть это утверждение неверно, тогда в каждой клетке сидит не более одного кролика, и, следовательно, в 50 клетках — не более 50 кроликов, а их должно быть 51. Получили противоречие.
Решение задачи с помощью принципа Дирихле сводится к выбору «кроликов» и «клеток». Иногда не совсем очевидно, кто в данной задаче является «кроликом», и что служит «клеткой».
1. Имеется 25 конфет 3 сортов. Верно ли, что не менее 9 из них будут какого-то одного сорта?
2. В классе 30 человек. Паша сделал 13 ошибок, а остальные меньше. Доказать, что какие-то три ученика сделали одинаковое количество ошибок.
3. В квадратном ковре со стороной 1 м моль проела 51 дырку (дырка — точка). Докажите, что некоторой квадратной заплаткой со стороной 20 см можно закрыть не менее трёх дырок.
4. a) Докажите, что в любой футбольной команде есть два игрока, которые родились в один и тот же день недели.
б) Докажите, что среди жителей Москвы найдутся десять тысяч, празднующих день рождения в один и тот же день.
5. В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее число шариков нужно вынуть из мешка вслепую так, чтобы среди них заведомо оказались два шарика одного цвета?
6. В лесу растет миллион елок. Известно, что на каждой из них не более 600000 иголок. Докажите, что в лесу найдутся две елки с одинаковым числом иголок.
7. Можно ли разложить 44 шарика на 9 кучек так, чтобы количество шариков в разных кучках было различным?
8. 100 человек сидят за круглым столом, причем более половины из них — мужчины. Докажите, что какие-то двое мужчин сидят друг напротив друга.
9. Докажите, что среди любых шести целых чисел найдутся два, разность которых кратна 5.
10. Докажите, что на шахматной доске нельзя расставить более 8 ладей так, чтобы никакие две из них не били друг друга.
11. Докажите, что никакая прямая не может пересекать все три стороны треугольника.
12. Обязательно ли среди двадцати пяти "медных" монет (т.е. монет достоинством 1, 2, 3, 5 коп.) найдётся семь монет одинакового достоинства?
13. Зайчиха купила для своих семерых зайчат семь барабанов разных размеров и семь пар палочек разной длины. Если зайчонок видит, что у него и барабан больше, и палочки длиннее, чем у кого-то из братьев, он начинает громко барабанить. Какое наибольшее число зайчат сможет начать барабанить?
14. По кругу выписано несколько натуральных чисел, каждое из которых не превосходит одного из соседних с ним. Докажите, что среди этих чисел точно есть хотя бы два равных.
15. Гоша задумал четыре неотрицательных числа и посчитал их всевозможные попарные суммы (всего 6 штук). Какие числа он задумал, если эти суммы — 1, 2, 3, 4, 5, 6?
16. В ящике лежат шары: 5 красных, 7 синих и 1 зеленый. Сколько шаров надо вынуть, не глядя, чтобы наверняка достать 2 шара одного цвета?
17. Каждая клетка таблицы 2015×2015 покрашена в один из 2014 цветов. За ход можно взять строку или столбец и, если там есть две клетки одного цвета, перекрасить эту строку или столбец в этот цвет. Можно ли за несколько ходов покрасить всю таблицу в один цвет?
18. Доказать, что среди 11 чисел всегда можно найти два таких числа, разность которых кратна 10.
Дополнительный материал можно найти здесь:
